ym>>Fakta menunjukkan bahwa di negeri kita saat ini banyak tumbuh dan bermunculan lembaga-lembaga yang menamakan dirinya sebagai lembaga bimbingan belajar. Atau, saya lebih senang menyebutnya sebagai lembaga bimbingan tes. Utamanya, lembaga semacam ini menawarkan jasa pada siswa-siswa sekolah berupa iming-iming keberhasilan dalam menempuh ulangan umum sekolah, ujian akhir sekolah, ujian akhir nasional, ataupun ujian masuk perguruan tinggi (negeri).
Yang dilakukan lembaga-lembaga bimbingan tes untuk menyedot siswa agar “bergabung” dengan mereka biasanya adalah dengan cara menawarkan strategi-strategi praktis dalam menghadapi tes, ulangan, ataupun ujian. Strategi-strategi praktis itu bisa berupa: stategi menjawab soal-soal, atau juga penggunaan rumus-rumus “cepat” untuk menyelesaikan soal-soal khususnya pelajaran matematika atau IPA (fisika ataupun kimia).
Dari ngobrol-ngobrol dengan beberapa siswa yang pernah menjadi peserta di lembaga bimbingan tes, saya memperoleh beberapa informasi penting. Katanya, yang paling membuat mereka tertarik “bergabung” adalah karena di bimbingan tes mereka dilatih untuk menyelesaikan soal-soal (baik matematika, fisika, kimia atau yang lainnya) dengan menggunakan rumus-rumus “cepat”. Sehingga dalam waktu singkat dapat menyelesaikan soal-soal yang diujikan. Selain itu, mereka juga dilatih tips and trik menjawab berbagai jenis soal. Pokoknya katanya, cara menjawab soal-soal yang dilatihkan itu sangat berbeda ketimbang yang diajarkan di sekolah. Di sekolah, misalnya untuk menjawab soal A perlu proses yang panjang dan berliku, sedang di bimbingan tes soal A dapat diselesaikan hanya dalam satu atau dua baris langkah pengerjaan saja.
Sedangkan dari beberapa diktat yang dikeluarkan lembaga-lembaga bimbingan tes tersebut saya pun bisa dapatkan informasi penting lainnya. Dari pengamatan saya, isi diktat-diktatnya berupa: rangkuman materi + rumus-rumus “biasa” + rumus-rumus “cepat” dan ratusan hingga ribuan latihan soal-soal beserta kunci jawabnya. Namun sayang, kata teman saya yang merupakan pengajar di salah satu bimbingan tes ternama di negeri ini, rumus-rumus “cepat” yang tertulis di diktat-diktat tersebut hanyalah rumus-rumus “cepat” yang sudah beredar secara luas. Sedangkan rumus-rumus “cepat” yang super “cepat” tetap dirahasiakan, tak dipublikasikan untuk umum. Hanya para perancang rumus, pengajar, dan siswa-siswa yang “bergabung” di tempat mereka saja yang tahu. Lebih lanjut katanya, masing-masing lembaga bimbingan tes mempunya rumus-rumus super “cepat” sendiri-sendiri hasil kreasi tim mereka, yang tentunya saling mereka rahasiakan.
Dari uraian di atas, tampaknya faktor penggunaan rumus-rumus “cepat” bagi suburnya perkembangan lembaga bimbingan tes cukup sentral, sangat penting. Walau mungkin bukanlah faktor utama. Sehingga, dapat dikatakan bahwa penggunaan rumus-rumus “cepat” bisa dijadikan salah satu faktor penting untuk memikat siswa agar mau “bergabung” mengikuti bimbingan tes.
Bicara tentang rumus-rumus “cepat” dan penggunaannya untuk menjawab tes, ada pro dan kontranya. Banyak yang pro tapi tak sedikit juga yang kontra. Dari hasil pengamatan pribadi dan ngobrol-ngobrol, saya bisa menuliskan beberapa alasan pihak yang pro dan yang kontra tersebut seperti berikut ini.
Beberapa alasan orang-orang yang pro terhadap penggunaan rumus-rumus “cepat” (matematika, fisika, kimia) itu di antaranya:
- Membantu siswa dengan cepat berhasil dalam menjawab tes (ulangan, ujuan sekolah, ujian masuk perguruan tinggi).
Sulit untuk dimungkiri bahwa dengan adanya rumus-rumus “cepat” banyak siswa yang terbantu dalam menjawab soal-soal tes dengan cepat. Membantu siswa melewati “jembatan” kelulusan sekolah. Pun membantu mengantar para siswa meraih cita-citanya untuk masuk ke perguruan tinggi idamannya.
Sebagai contoh, perhatikan satu soal berikut:
Soal: Jika 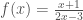 maka
maka 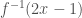 =….
=….
Bila kita menggunakan cara biasa, perlu lebih dari tiga “baris = langkah” untuk menyelesaikannya. Sedangkan bila memakai rumus “cepat” soal semacam ini bisa diselesaikan hanya dengan dua “baris =langkah” pengerjaan.
Dengan contoh-contoh penggunaan rumus-rumus “cepat” semacam ini, siswa mana yang tak terpikat menggunakannya?
- Membantu pemerintah untuk mengurangi pengangguran.
Bagaimana bisa penggunaan rumus-rumus “cepat” bisa membantu mengurangi pengangguran? Seperti yang sudah diuraikan di atas, dengan adanya rumus-rumus “cepat” perkembangan bimbingan tes makin subur. Nah, karena saking tumbuh suburnya, tentu lembaga-lembaga ini butuh tenaga pengajar. Karena itulah banyak lulusan perguruan tinggi yang belum dapat pekerjaan biasanya dengan rela hati menjadi pengajar atau perancang soal di lembaga semacam ini. Sementara mencari pekerjaan tetap, mereka bisa sambil bekerja di lembaga-lembaga bimbingan tes. Bahkan banyak juga yang akhirnya memutuskan untuk menjadi pengajar saja, dan (mungkin) pelan-pelan melupakan bidang keahliannya yang pernah ditekuninya semasa di perguruan tinggi dulu. Selain pengajar atau perancang soal, tentunya sang pemilik lembaga semacam ini sebagai pelaku busines juga terbantu. Mereka punya lahan baru dalam dunia beginian. Busines dalam di dunia pendidikan.
- Meningkatkan kreativitas perancang rumus-rumus “cepat”, pembuat soal, dan para “businessman” pendidikan.
Biasanya, para perancang rumus-rumus “cepat” atau pembuat soal itu adalah orang-orang luar biasa di bidangnya. Mungkin sebelum adanya lembaga bimbingan tes, rumus-rumus “cepat” hasil kreasi mereka hanya dipakai untuk kalangan pribadi. Tapi kini, dengan adanya lembaga bimbingan tes, kreasi mereka tersalurkan. Mereka semakin tertantang untuk menemukan umus-rumus “cepat” baru untuk menjawab soal. Mereka juga terpacu membuat soa-soal baru yang mungkin hanya bisa diselesaikan dengan rumus-rumus baru temuan mereka. Untuk menambah kredibilitas lembaga bimbingan tes, tak sungkan-sungkan para perancang rumus-rumus “cepat” atau pembuat soal itu oleh sang businessman diambil dari kalangan perguruan tinggi (ternama).
Para businessman pendidikan pun akan makin terpacu untuk memasarkan jasa mereka ke konsumen. Dengan segenap kemampuan, mereka menggembor-gemborkan jasanya. Tentunya kreativitas dan strategi pemasaran sangat dibutuhkan dalam hal ini.
Mungkin saja Anda yang pro terhadap penggunaan rumus-rumus “cepat” ini mempunyai alasan lain. Silakan menambahinya di kolom komentar!
Sedangkan bagi mereka yang kontra alias tak setuju dengan penggunaan rumus-rumus “cepat” juga mempunyai alasan-alasan. Beberapa alasan tersebut di antaranya seperti berikut ini.
- Menjerumuskan siswa ke jurang kebodohan
Bila dilihat sepintas, penggunaan rumus-rumus “cepat” sepertinya cukup membantu siswa untuk berhasil dalam ulangan ataupun ujian. Namun, sebenernya seringkali bisa menjerumuskan siswa ke jurang kebodohan bila penggunaannya tak dilandasi oleh pemahaman, hanya mengandalkan hafalan rumus tanpa pengertian. Ini artinya, proses berfikir tak begitu diperhatikan, tidak dianggap penting. Akibatnya siswa-siswa terbiasa cepat ingin ketemu hasil akhir, maunya serba instant, ingin mudah dan cepat tanpa mau bersusah payah.
Secara ekstrem, ada kawan saya yang mengatakan bahwa penggunaan rumus-rumus “cepat” harusnya dilarang keras, karena sebenarnya merupakan cara-cara yang mengarah pada pembodohan generasi penerus bangsa. Juga katanya, mungkin saja benar bahwa dengan menggunakan rumus-rumus “cepat”, banyak siswa terbantu bisa masuk perguruan tinggi idamannya. Tapi, bantuan yang diberikan itu sangat tanggung, setengah-setengah. Ibaratnya, setelah siswa diantar masuk perguruan tinggi misalnya, siswa dibiarkan begitu saja, dibiarkan terjerumus, dibiarkan secara tak bertanggung jawab.
Di satu kesempatan lain, saya pernah mendengar cerita bahwa di salah satu perguruan tinggi, siswa-siswa produk bimbingan tes yang terbiasa menggunakan rumus-rumus “cepat” tanpa dilandasi pemahaman banyak yang kesulitan mengikuti perkuliahan, bahkan banyak di antara mereka terpaksa DO (Drop Out) tak sanggup mengikuti materi perkuliahan. Sedangkan siswa-siswa yang secara alami tak tercemar oleh bimbingan tes justru berhasil dengan baik dalam belajarnya.
- Merusak tercapainya tujuan pendidikan
Tujuan pendidikan secara umum, biasanya tertuang di kurikulum pendidikan, ringkasnya adalah, “untuk mengembangkan sumberdaya manusia yang kreatif, konstruktif, produktif, bertanggung jawab, berdisiplin, beriman dan bertakwa.” Nah, apakah dengan penjejalan penggunaan rumus-rumus “cepat” pada siswa tanpa dilandasi pengertian memungkinkan tercapainya tujuan tersebut?
Bagi pembaca yang kontra alias tak setuju dengan penggunaan rumus-rumus “cepat” silakan menambahi alasannya!
Nah, kalau saya sendiri termasuk yang pro atau yang kontra nih? 
Ya sudah segitu dulu saja, sampai jumpa di tulisan berikutnya.
Catatan: Rumus-rumus cepat yang saya maksud bisa berupa rumus-rumus cepat dalam matematika, fisika, kimia, atau mata pelajaran lainnya.


